As developers, all of us will sometimes come along with a problem that will make you think out of the box. For me, one of such problems was a situation where I had to get a valid response based on six different variables that depended on each other’s state. All of them were on top of some logic that was already complicated. At that point, I didn’t even know how to begin to write conditions. Knowing even less how to ensure that the result was always correct. We did solve the problem in the end by using Boolean Algebra, and explained below is the process of how to do it.
The example
For the sake of the example, let’s say I walk into an imaginary library where the only possible genres are fantasy and romance. I want to choose some books to read, but I have my standards:
- I like romance books only if they are also fantasy books, but I don’t want to read a book that is shorter than 200 pages or longer than 800 pages.
- Fantasy books are amazing and I don’t care about their length, but I don’t want romance in that case,
- If a book is shorter than 200 pages or longer than 800 pages, I want it to be of the romance genre.
Since there are a lot of books to go through, I want to create a program which will filter out all of the books to my liking. Shown below is the list of conditions each book has to pass to be declared as a book that I would like to read:
if (
($book->isFantasy() && $book->isRomance() &&
$book->getLength()>200 && $book->getLength()<800)
||
($book->isFantasy() && !$book->isRomance())
||
($book->isRomance() && ($book->getLength()<200 || $
book->getLength()>800))) {
return $book;
}Well, this looks overly complicated. Imagine just what it would look like if we added a third genre with its own constraints…
Did you imagine it?
At this point, we could shape all the conditions in the way they are represented with a boolean value, which would then shorten the code a bit. Keeping that in mind, we could change the book-length constraints to look like this:
$isLengthWithinRange =
$book->getLength() > 200 && $book->getLength() < 800;
if (
($book->isFantasy() && $book->isRomance() && $isLengthWithinRange)
||
($book->isFantasy() && !$book->isRomance())
||
($book->isRomance() && !$isLengthWithinRange)) {
return $book;
}This is a bit easier to understand, but it would still be a nightmare to maintain. On the bright side, all of our constraints are now represented by a boolean algebra variable. This reminded me of Boolean algebra and minimizing boolean algebra functions that I learned at college. To be fair, at the time I thought I would never really use it.
After changing the conditions
The book’s validity depends on 3 boolean variables. This leads to 2³ = 8 different combinations. The next step is to draw a truth table and fill in all the combinations and the output function (you can find more on boolean logic and truth tables here).
The combinations of variables that indicate that the book passes all the conditions should be marked with 1. On the other hand, invalid combinations should be marked with 0. If you have some combinations that are impossible to happen in real life (or code), like a book that is neither of romance nor fantasy genre – you can mark them with R or X (redundant/“don’t care”). Marking some combinations as redundant can shorten or lengthen your minimized function, so you can experiment with this one.
Here is the truth table written based on constraints in the library example:
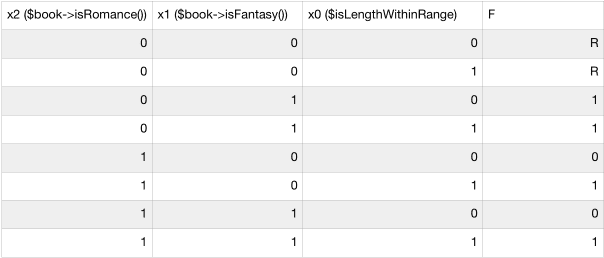
From the table we can see four valid situations:
- a book is in the fantasy genre, everything else is false
- the book is of the fantasy genre and valid in length
- a book is of the romance genre and is valid in length
- the book is of romance and fantasy genre and is valid in length.
The case where all the variables are false is consequently impossible, and is marked as redundant. The same goes for the case where both book genres are false. Every other outcome is not valid. Due to the whole table being filled in, you will get your output function (marked with F in the table). As you can see, we still have 4 different conditions, so the next step is to minimize the output function.
There are a number of different ways which you can use to minimize the function. I strongly prefer using the Karnaugh-Veitch map. If you are not familiar with Veitch diagram or other minimizing algorithms – do not worry! The internet is your saviour. I find this tool really easy to use, therefore it tells you where every value of the output function goes and it’s pretty straight-forward. If you use redundant output function values, make sure to mark “Allow don’t care” checkbox.
Karnaugh-Veitch map
In this map type, every row from a truth table is represented by a cell position in a two-dimensional grid. The value of the cell is the output function value of the corresponding row in the truth table. To minimize the output function, we have to find optimal groups of valid results. Redundant values can be grouped either with valid or invalid results.
What you basically do here is the group the valid conditions. Try to do it in a way that each group covers the most
After filling in the output function from the table above, the Karnaugh-Veitch diagram looks like this:
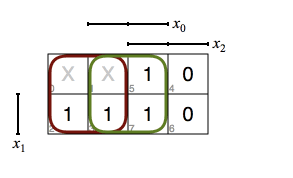
As a result, the circled areas represent the minimized function, which is:
F = (x̄2) ∨ (x0), where x2 is $book->isRomance() and x0 is $isLengthWithinRange.This can easily be translated into conditions, like so:
$isLengthWithinRange =
$book->getLength() > 200 && $book->getLength() < 800;
if (!$book->isRomance() || $isLengthWithinRange) {
return $book;
}All in all…
As a result, now you have your minimal set of conditions that will always provide you with a valid result. If you sit and think hard about the constraints we had in the beginning, you would probably come to a solution similar to the resulting minimized function after some time.
But why waste your time and brain cells when you can use existing algorithms and techniques that will save you a lot of time? Long live Boolean algebra!